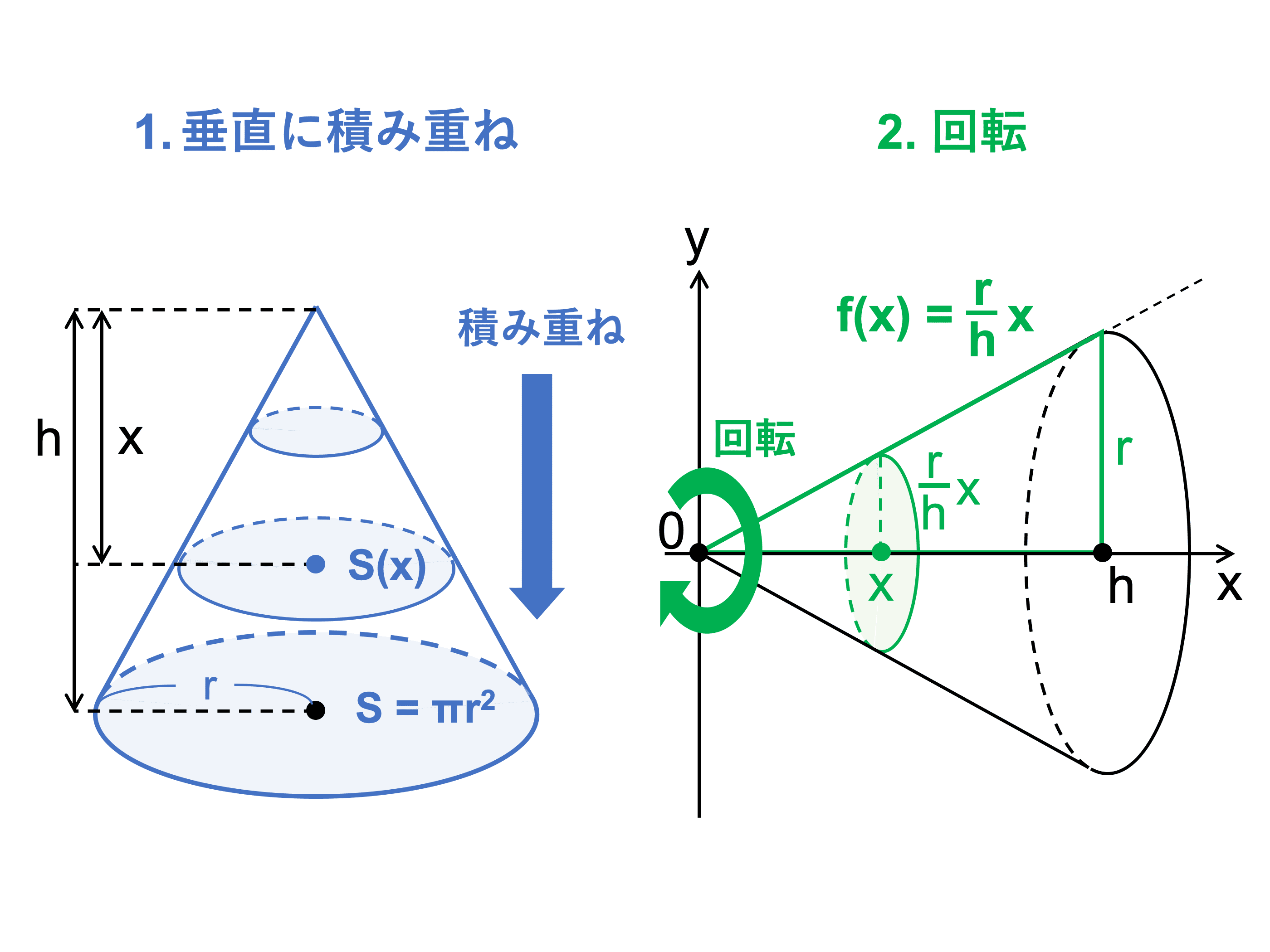
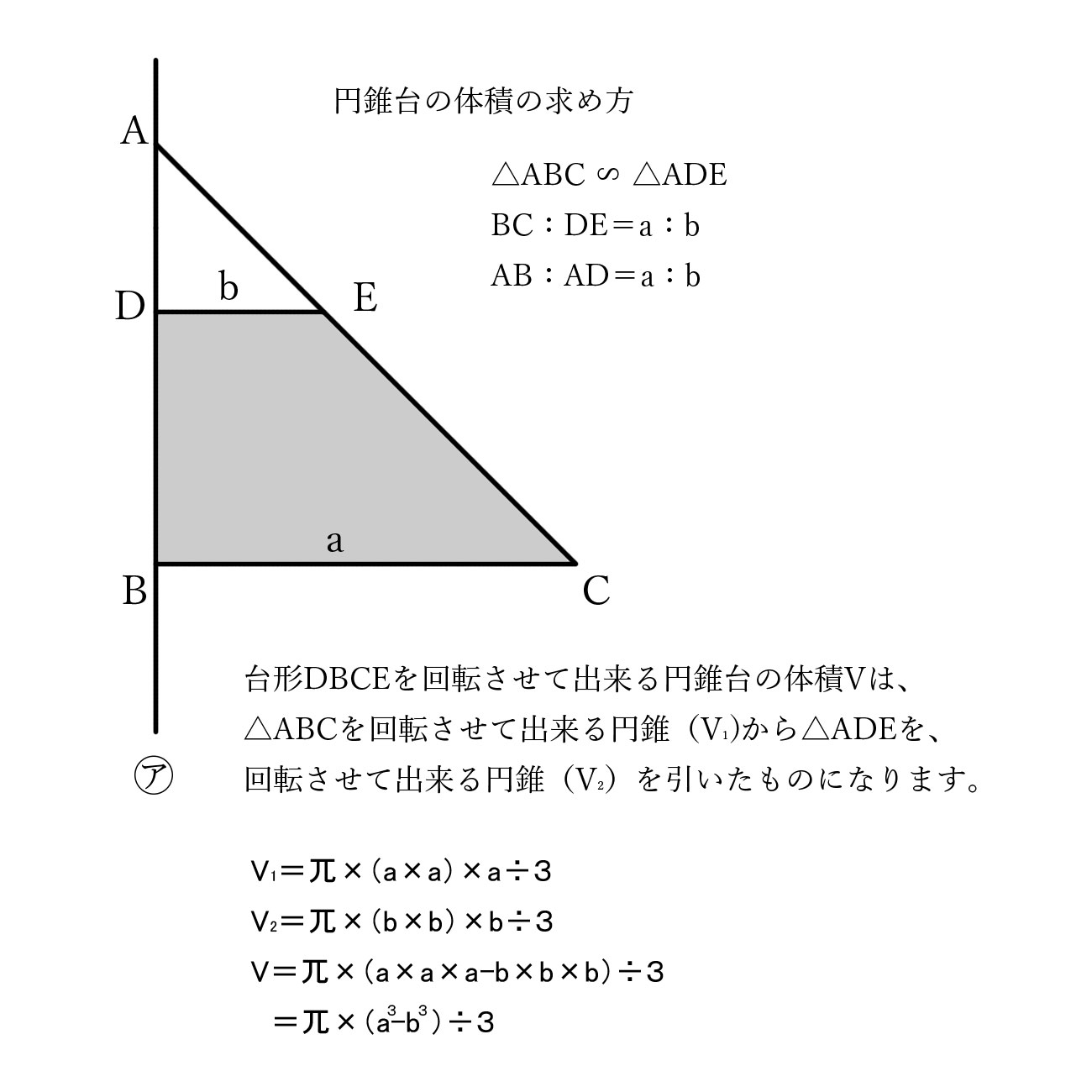
· 円錐の体積を円柱座標系で真面目に計算してみた よく知られているように、円錐の体積は 1 3πR2h 1 3 π R 2 h です。 ここで底面の円の半径を R R 、高さを h h としました。 中学の数学などで天下り的に教わったのですが、導出は教わった記憶がありませんX h = b h a − b ( a − b) h a − b = a h a − b となります。 したがって、大きな円錐の体積は、 π a 2 × a h a − b × 1 3 = π a 3 h 3 ( a − b) となります。 よって、円錐台の体積は「大きな円錐の体積」から「小さな円錐の体積」を引いたものなので、 ( a 3 − b 3) π h 3 ( a − b) = 1 3 π h ( a 2 a b b 2)『円錐の体積が円柱の1/3なのはなぜなの?』 1、三角形と錐体を比べる t:こういう時は、よく知っているものと比べながら考えるとわかるよ。錐体は何かと似ていない? s:三角形だ。 t:そうだね。「三角形と四角形」は「錐体と柱」に似ている。 例えば、三角形は高さが同じなら頂点を

マンスリーミニ対策 円錐台 中学受験 プロ家庭教師 コージー先生の独り言
円錐台 体積 求め方
円錐台 体積 求め方-円錐の体積の求め方を確認しておくと こうでしたね。 コレに当てはめて考えていきましょう。 底面積は円の面積公式\(\pi r^2\)に当てはめて $$\pi \times 4^2=16\pi$$ となるので、体積は $$16\pi \times 4\sqrt{3} \times \frac{1}{3}$$ $$=\frac{64}{3}\sqrt{3}\pi cm^3$$ となりました。 三平方の定理を使って 高さを · 円錐の体積の求め方の公式 は、 底面積×高さ×1/3




17 号 フレキシブル基板及びそれを用いてなる円錐台形状の回路基板 Astamuse
NeKo_quatre ベストアンサー率44% (509/1134) > 05÷1 shift特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くことも 75 三角 錐 体積 の 求め 方 四角錐台の体積 高精度計算サイト 簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを 簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。
1612 · 立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 高さの分からない円すい展開図 どうやって立体の体積を求めるの 円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生 円錐の表面積の求め方は完全パターン化できる 円錐 中心角 求め方 角錐と円錐の体積 Youtube円錐の母線、半径、中心角の関係式とそれぞれの求め方 具体例で学ぶ数学 > 図形 > 円錐の母線、半径、中心角の関係式とそれぞれの求め方 最終更新日 r = l × x 360 という式を使うことで、 母線の長さ l 、 底面の半径 r 、 側面のおうぎ形の中心角 · 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。 今日は、この公式で体積を計算してみよう!! 使って覚えるのが一番だからね。
· 円錐の表面積は、上の公式を覚えておけば楽勝だよ♪ それでは、例題を使って円錐の表面積の求め方を確認してみましょう。 次の円錐の表面積を求めなさい。 まずは公式にしたがって円錐の底面積を求めましょう。 底面積 次は母線と半径をかけて体積 V = 1 3 π ( r 1 2 r 1 r 2 r 2 2) h · 円錐の体積の求め方 円柱・底面の半径が5cm高さが2cm 円錐・底面の半径が3cm高さが16.66・・・cm 円柱と円錐の体積が等しくなるときの円錐の体積は 何cm3になるのですか? 締切済み 数学・算数;
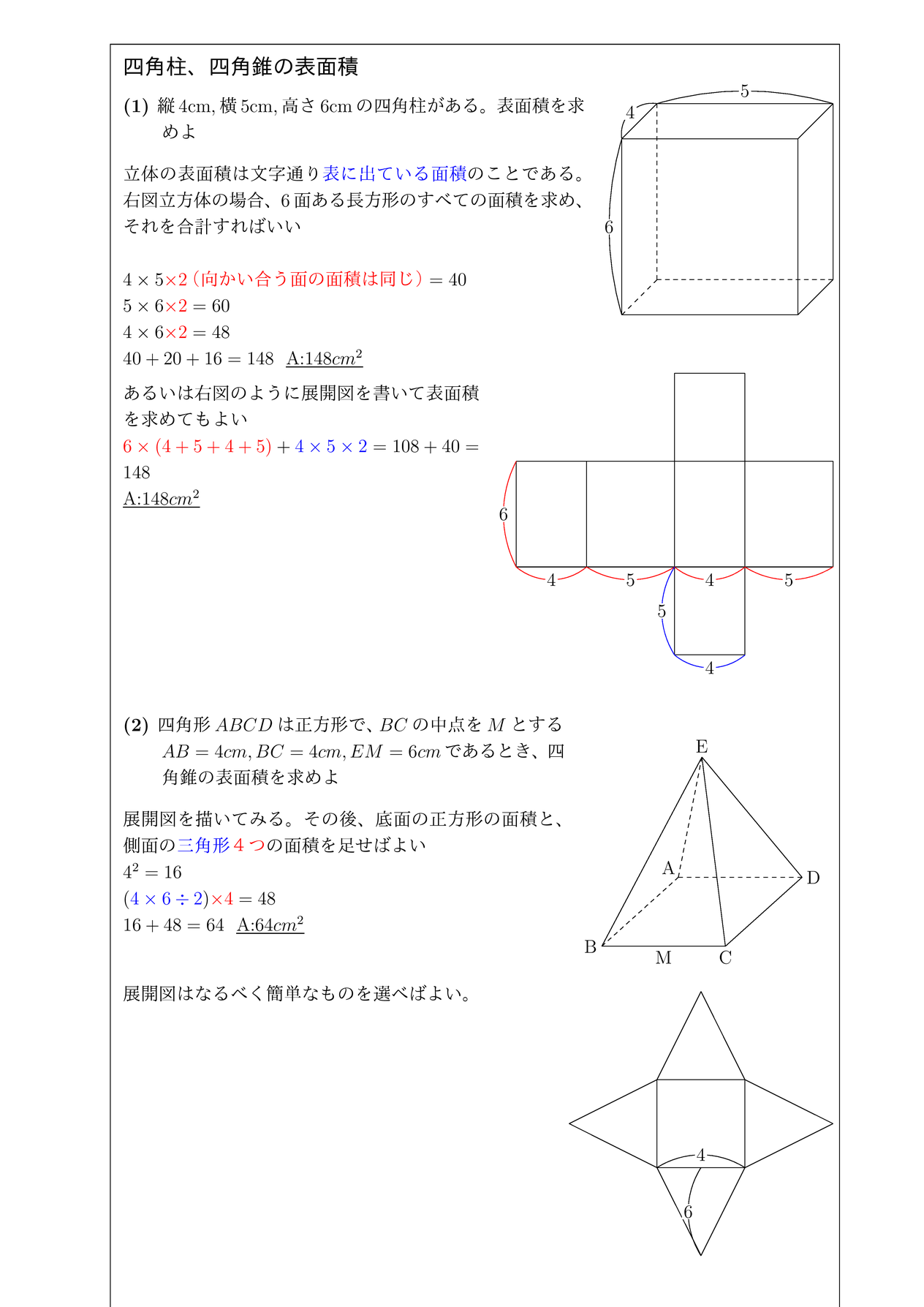



四 角錐 表面積




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
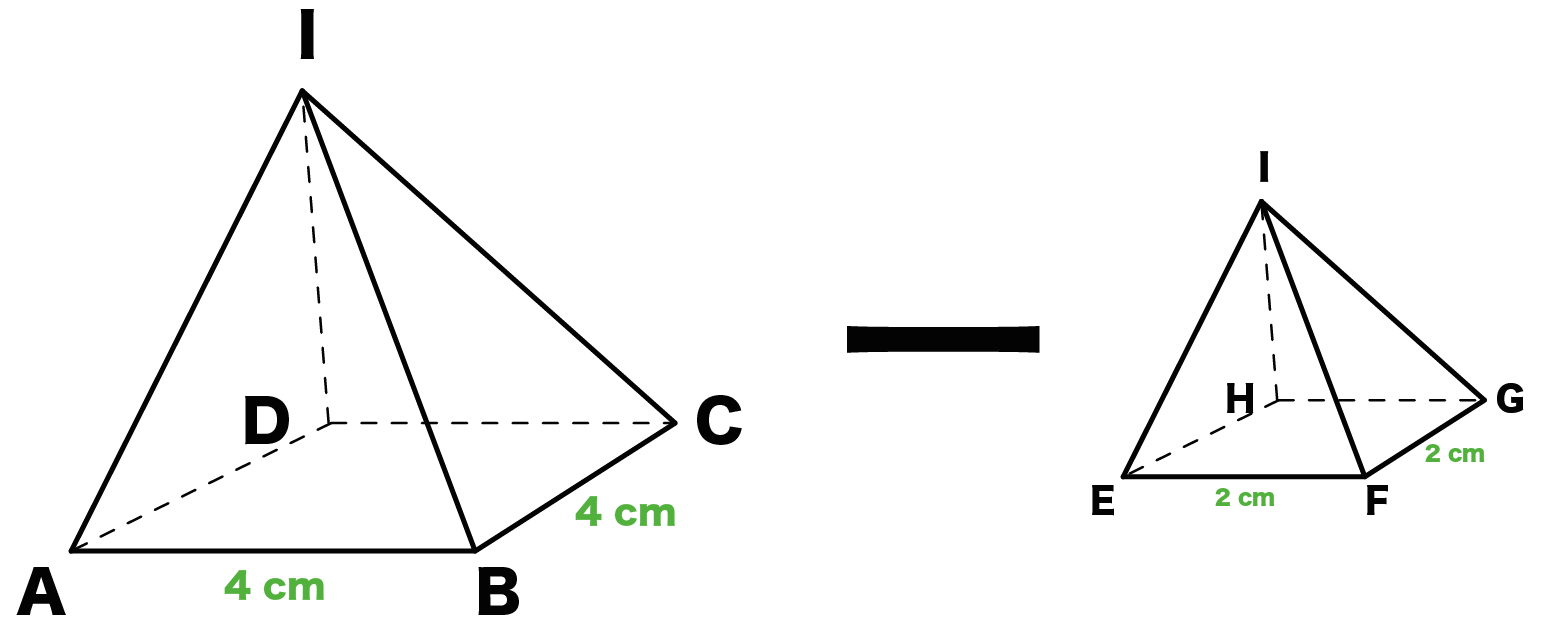
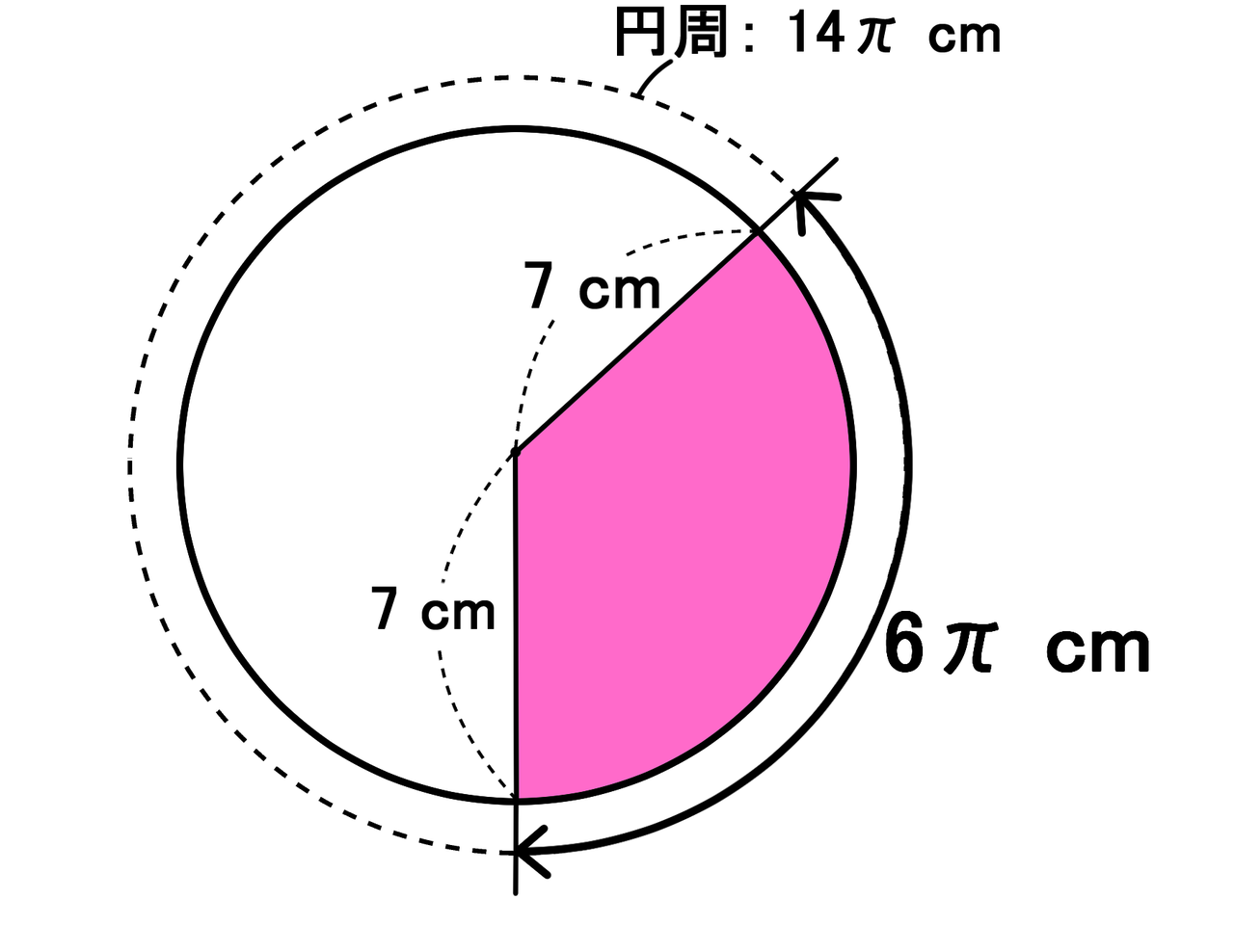
· 円錐台の体積の求め方 円錐台の体積の求め方についての質問です。 上底の半径=3 下底の半径=4 高さ=3 円周率=π この場合、大きな円錐の体積-小さな円錐の体積 という考え方や円錐 台の公式がある(正解は37π)ことは知っています 円錐台の体積の公式 S:はじめまして。いつもホーム · 円錐問題の考え方 円錐を2つに分けた図形の体積比を考えるのですが そもそも相似になっていません では、どのように考えていけば良いのかというと 一旦、このように小さな円錐と大きな円錐を考えてやります。 大きい方の円錐は③と①を合わせた辺になっているから④になるっていう円錐台の体積を求めて,次にこれから中空の円柱の体積を引くとよい. まず,比例(相似)の関係から ABBC=ADDE → 34=6DE → DE=8 次に,円錐台の体積 π×6cm 2 ×8÷3=96π (cm 3)から上端の円錐の体積 π×3cm 2 ×4÷3=12π (cm 3)を引いて 84π (cm 3)
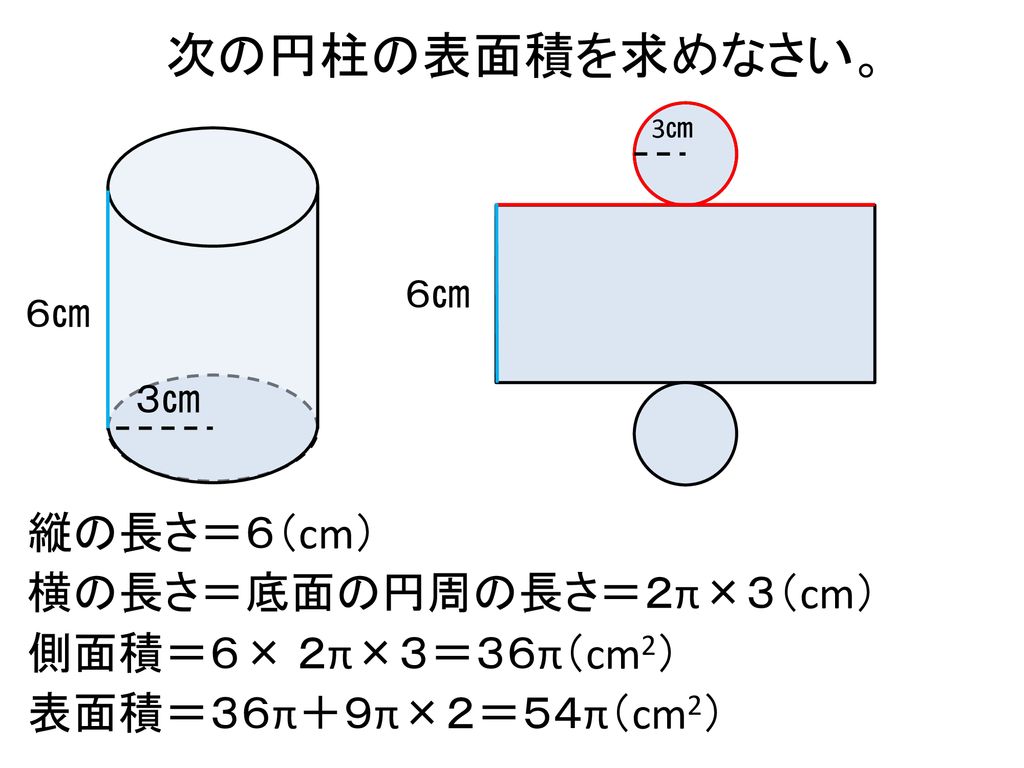



円柱 表面積




裏技 プリン型の立体の体積 一瞬で求められますか Youtube
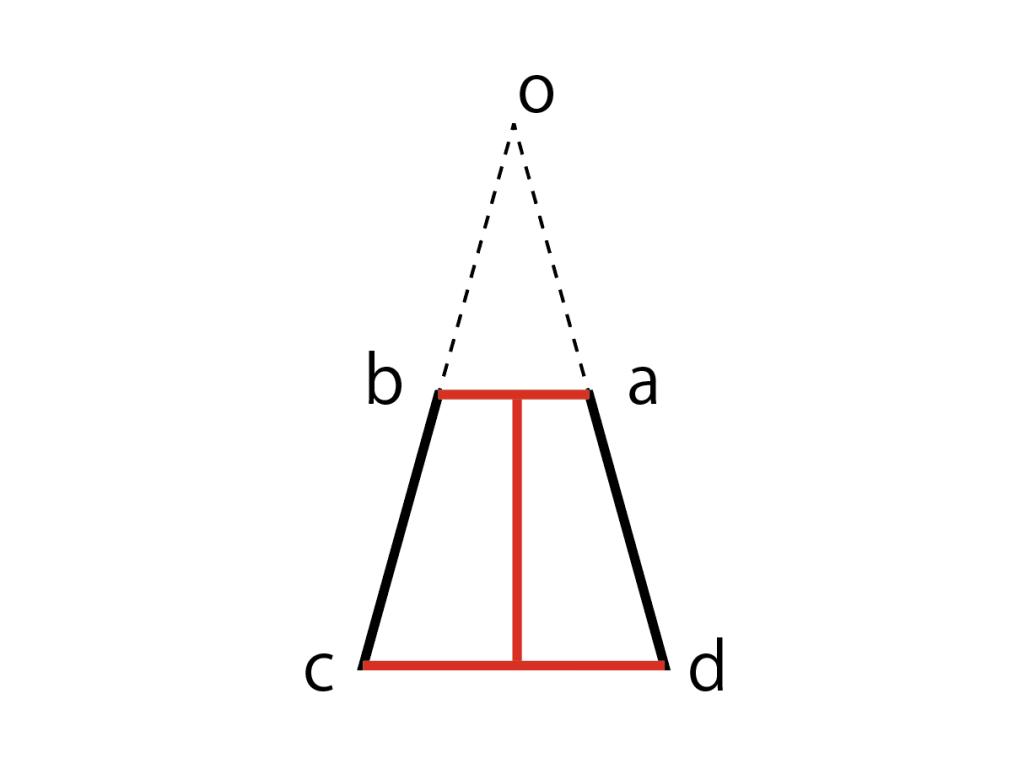
· 円錐の高さの求め方概要 円錐の高さを求める問題は、この2パターンくらいかな 母線と半径から、三平方の定理を使って求める 体積と半径から、円錐の体積の公式を使って求める 表面積と半径とかからも求められなくはないけど、複雑だから出ることは体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方 メインコンテンツに移動 製造現場の設計、加工、 保全技術から工具豆知識まで 検索 技術情報;円錐台(えんすいだい、英 circular truncated cone )は、円を底面とした錐台である。 つまり、円錐を底面に平行な平面で切り、小円錐の部分を除いた立体図形である。 プリンの形は一般的には円錐台である。受験数学、特に日本の中学入試でよく出題される図形である。




空間図形14 円すい台の体積 Youtube



花まるラボ スマホやタブレットで使える中学受験対策アプリ 究極の立体 展開 を発売 Edtechzine エドテックジン
8、円錐台の体積の公式 目次にもどる 人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。覚え方は、『3分で忘れる心配あーるの参上。』『身の上に心配あーるのさん一部が欠けた直円錐の体積 一部が欠けた直円錐の体積 直円錐の半径と高さから縦に切断した体積、底面積、側面積、切断面積を計算します。 円錐台の体積 円錐台の体積 円錐台の底面と上面の半径と高さから体積、側面積、表面積を計算します。 楕円錐の体積 楕円錐の体積 · 円錐の体積=底面積×高さ÷3なので 求める円錐の体積=5×5×314×9÷3=2355(cm³) 答え 2355cm³



双円錐 Wikipedia




四 角錐 表面積 プロジェクト ニュース
· 円錐 体積 の 求め 方 円錐 体積 の 求め 方まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi(cm^2)$$ 次は母線と半径をかけて、側面積を求めます。例 3 65 (円錐の体積) 底面の半径 ,高さ の円錐の体積は である. これを多重 · 円錐台の体積を計算する方法を教えてください。 上面の数値と高さと角度がわかっている場合の体積の求め方を教えてください。 上面直径が05cm高さが5cm角度が2°の場合の円錐台。cm3(立方センチメートル)での答えの導き方を途中式を略さずに教えて · よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式! ? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、




中1数学 円すいの体積 表面積の求め方と練習問題 Examee




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
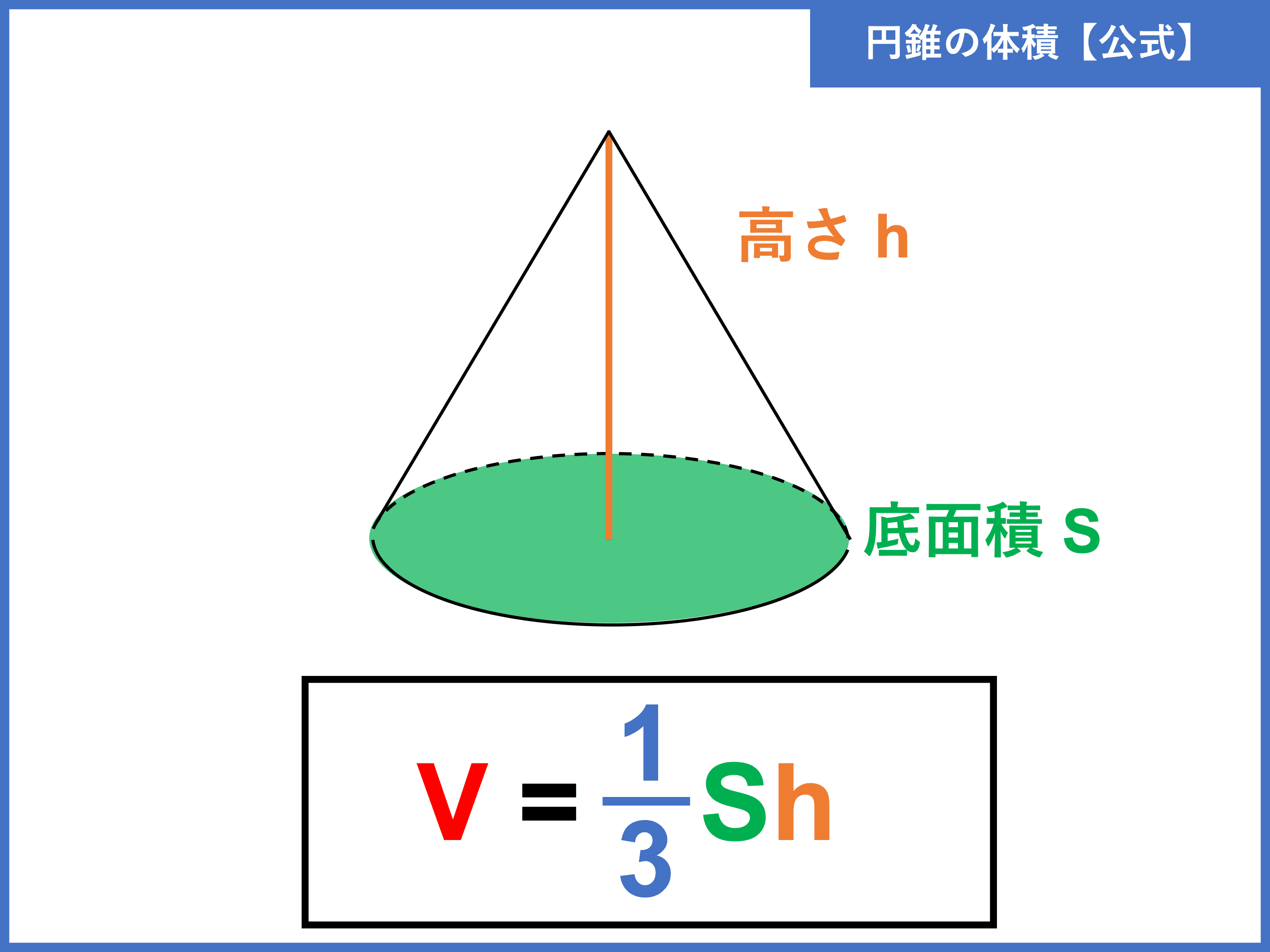
V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの問題図の円錐の体積を求めなさい。 ○錐の体積 → 底 面 積 高 さ 底面積 × 高さ × 1 3 V = 1 3 S h 円錐の底面は円なので、底面積は π π 3 × 3 × π = 9 π 高さは 4 c m0717 · すい体の体積の求め方 すい体とは、先がとがっている立体図形のことです。工事現場にあるような赤い三角コーン、エジプトのピラミッドなどをイメージしてもらえればお子さんにも伝わるかと思います。 すい体の体積=底面積×高さ÷3




至急 3 を教えて下さい 答えは64 63 倍です Clear




Solidworksで円錐台や円錐の作り方は
もっと見る その他の回答 (1) 25 回答No2;円錐台の底面と上面の半径と高さから体積、側面積、表面積を計算します。 円錐台の体積 高精度計算サイト ゲストさん · 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし




17 号 フレキシブル基板及びそれを用いてなる円錐台形状の回路基板 Astamuse




円錐の体積ってなんであの公式なの Webty Staff Blog
倍数 立方体・直方体の体積の概念 面積の意味と求め方 ★ 一般的に,日本のカリキュラムのうちの図形分野は海外に比べて進度が速い。 ★ 分数の概念が未習の場合,「×1/3」と「÷3」の対応関係や「3倍」との関係を丁 寧に指導する必要がある。日常では「AはBの倍です」というときは「2倍円錐台の体積を計算する Runcated cone 円錐台の体積は π ÷ 3 × ( r1 × r1 r1 × r2 r2 × r2 ) × 高さ で求めることができます。 底面半径 (r1) : 上面半径 (r2) : 高さ (h) : 体積 : 円錐台の体積 円錐台の表面積 円錐台の側面積 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差円錐の体積と表面積の求め方(公式)について、現役の慶應生がスマホでもパソコンでも見やすい図を使いながら解説 します。 この記事を読めば、数学が苦手な人でも円錐の体積・表面積の求め方(公式)が必ず理解できるでしょう。 超緊急です!!四




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




Android 用の 体積計算 Bynsdev Apk をダウンロード
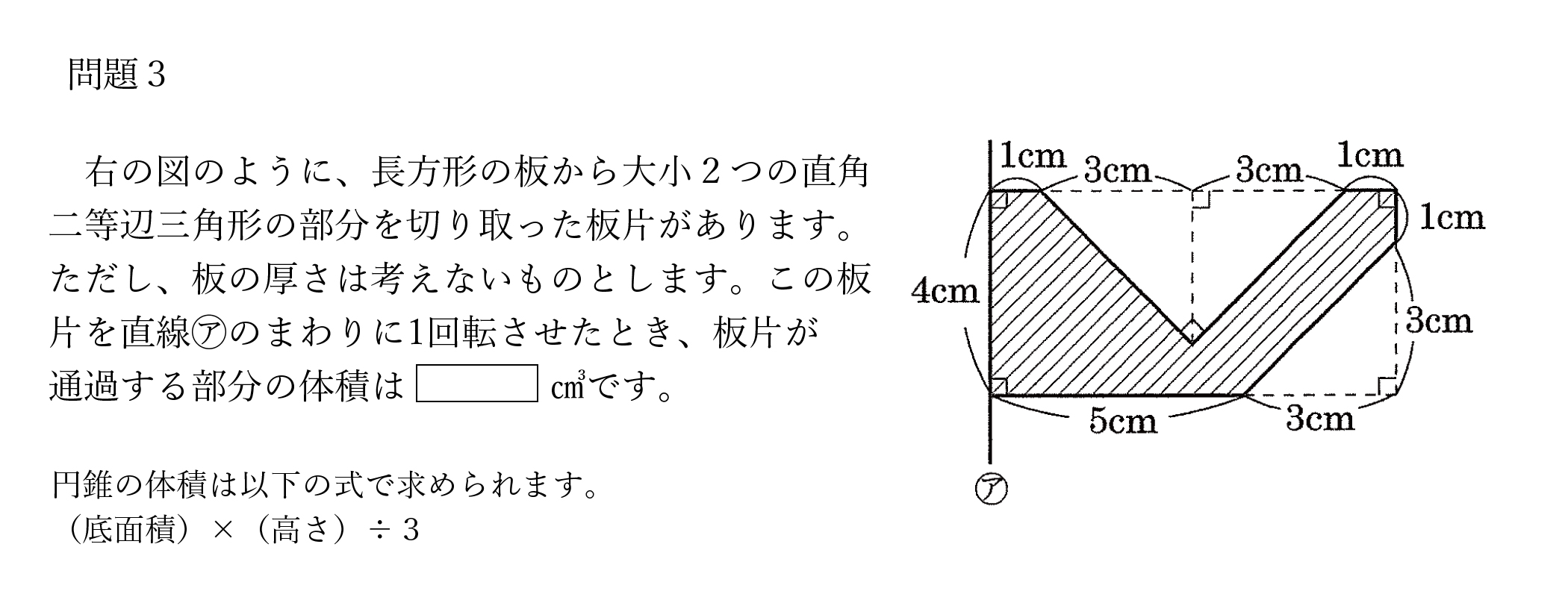



頭の体操 問題3 解答 Cometのサボテン栽培日記
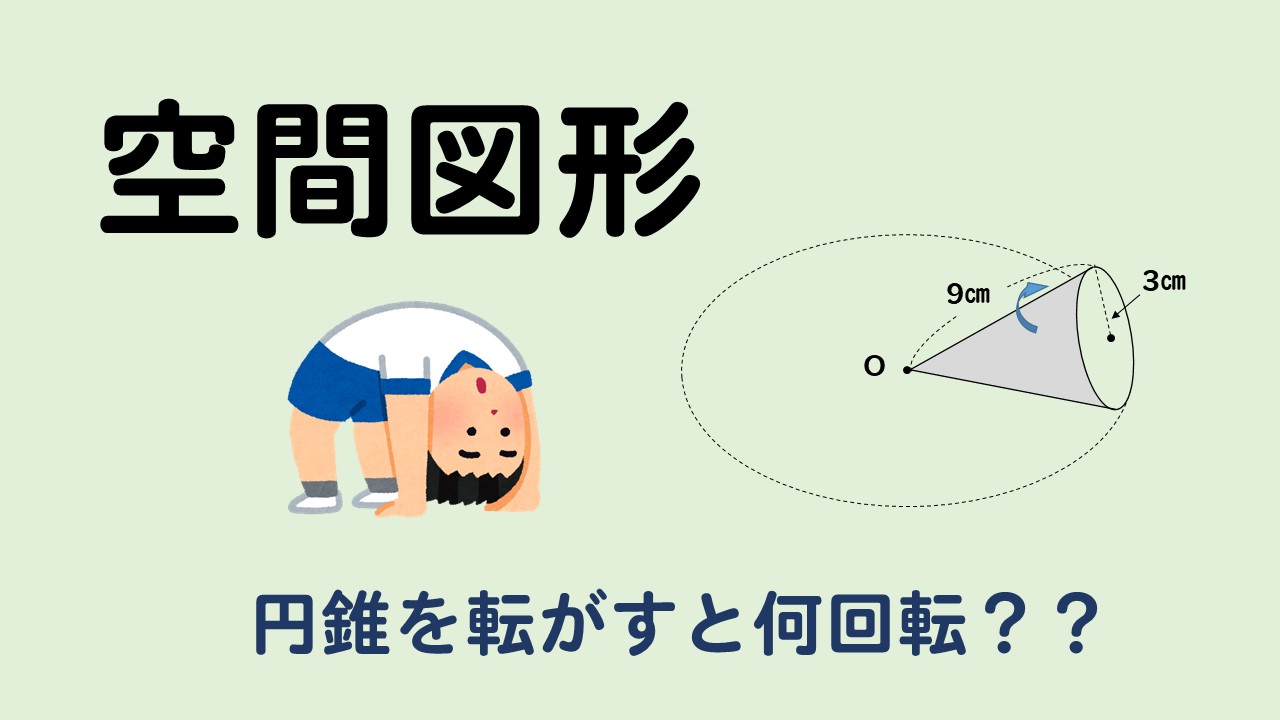



円錐を転がすと1周するのにどれくらい回転する 入試問題を解説 数スタ
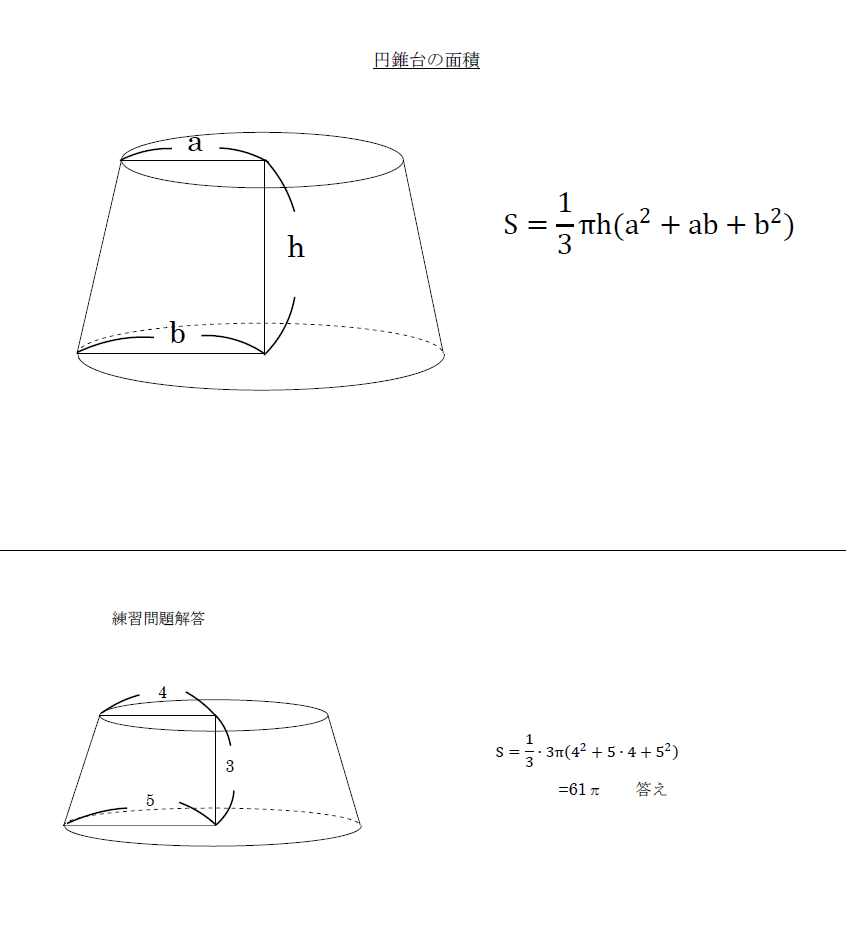



空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法




円錐 表面積 裏 ワザ




四角錐台の斜辺の長さ 四角錐台の斜辺の長さを教えて下さい 小さい四角 Okwave



変な形の体積を出したいのですが どなたかお願いします 変な形 Yahoo 知恵袋




斜軸回転体の体積 応用編 傘型積分 おいしい数学
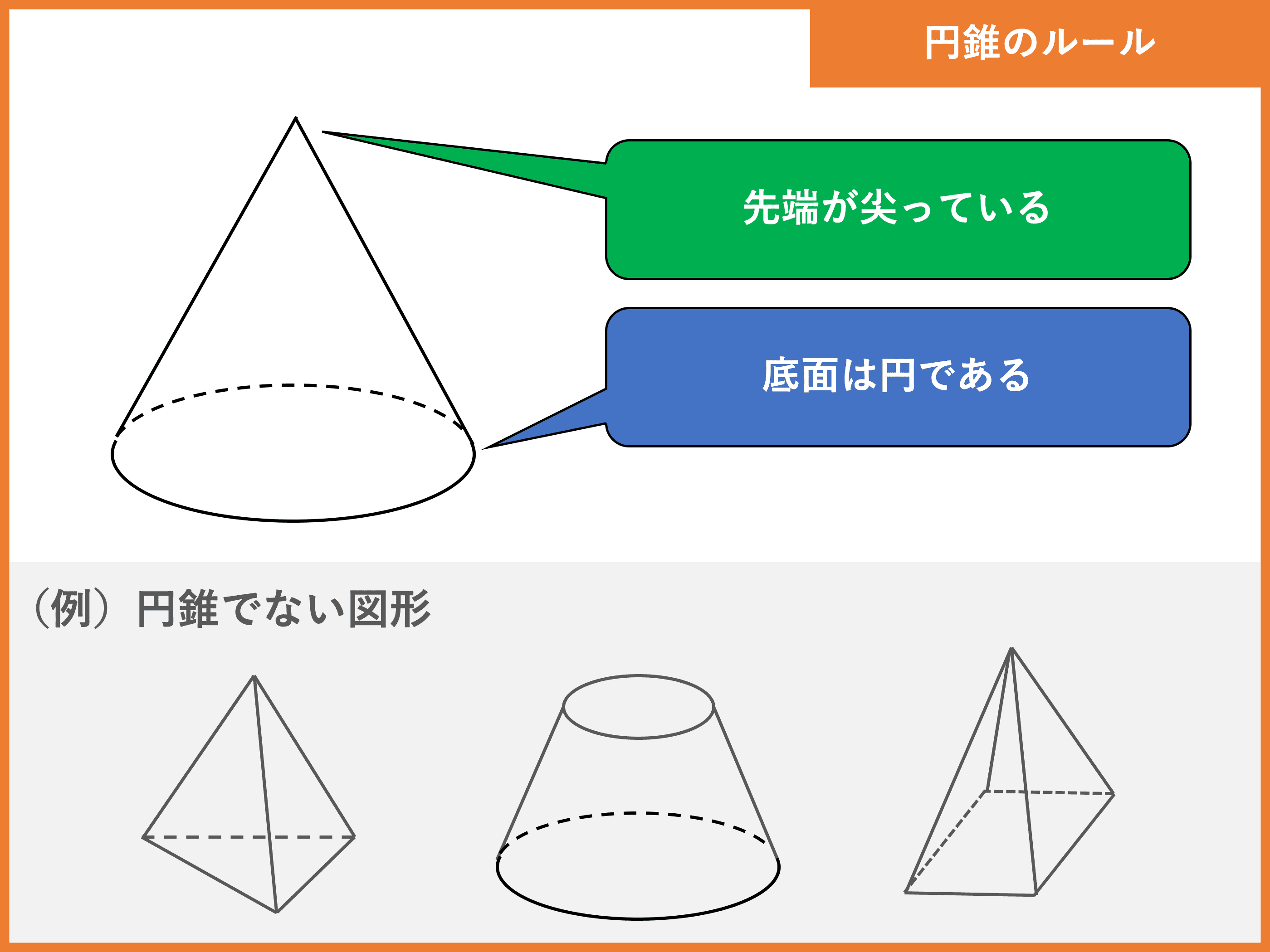



Pictngamukjpackh Achevee 円錐 体積 求め方 母線 円錐 体積 求め方 母線



立体図形 デジタル教科書 電子教科書




Images Of 円錐台 Japaneseclass Jp




中3 円錐台の体積 Youtube




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
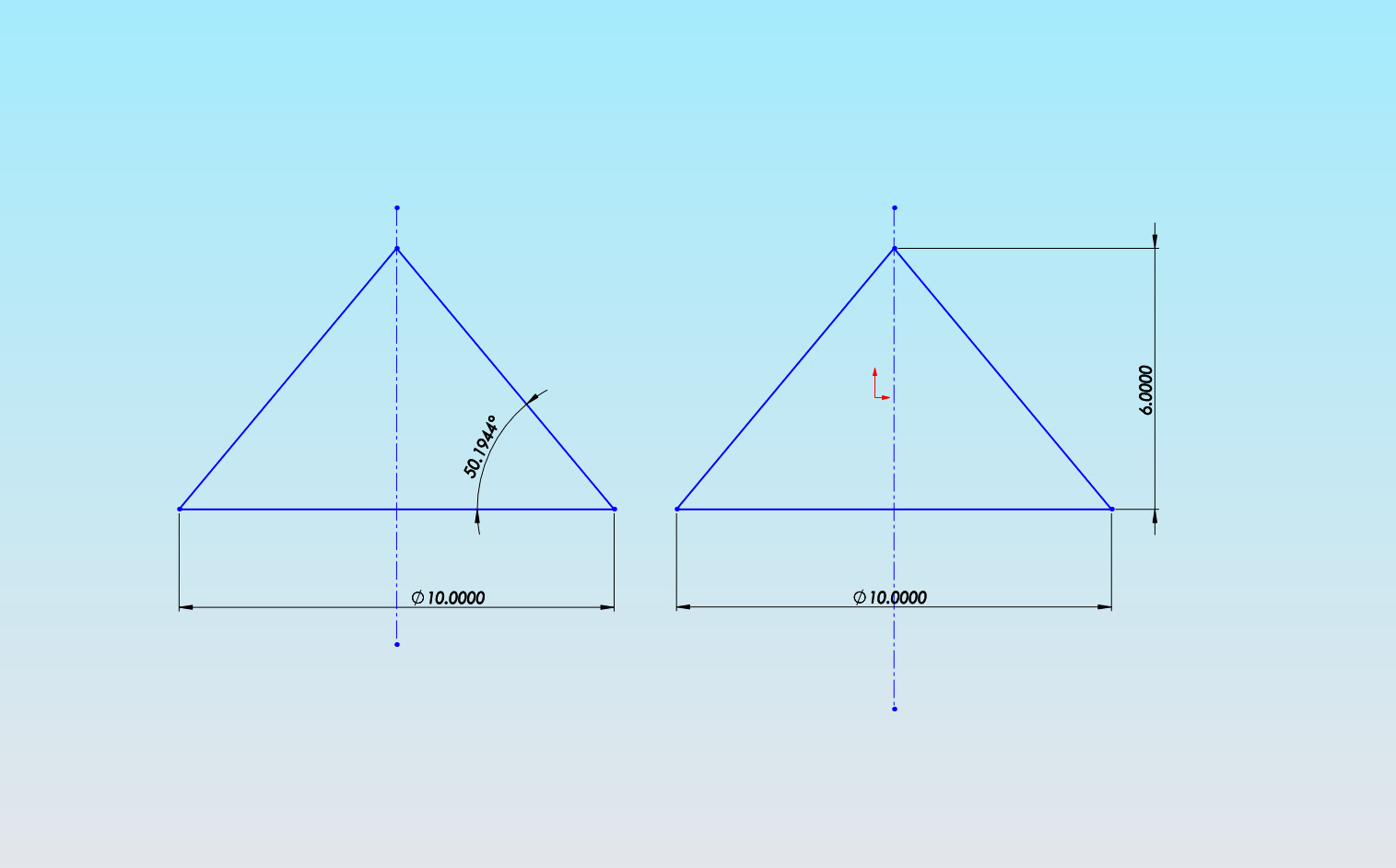



Solidworksで円錐台や円錐の作り方は



簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




立派な 台形 体積 求め 方




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



Pictngamukjpackh Achevee 円錐 体積 求め方 母線 円錐 体積 求め方 母線




円錐 の 側 面積 の 求め 方 円すいの展開図 側面積の求め方 公式を使って15秒で解こう




円錐の体積について 半径1の球に高さhの円錐が内接している 写真を参照 Okwave




円錐の表面積 Youtube



四角柱の体積 デジタル教科書 電子教科書




この2つは どのやって求めればいいんですか 解き方を教えてください Clear




マンスリーミニ対策 円錐台 中学受験 プロ家庭教師 コージー先生の独り言




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




100 Epic Best円錐 の 体積 公式 最高のぬりえ




円錐や角錐の体積の求め方 中学1年数学 Youtube




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




台形 体積 求め 方 円錐台の体積と表面積を計算する公式と証明




成城中 算数の図形問題 プロが教える重要ポイント
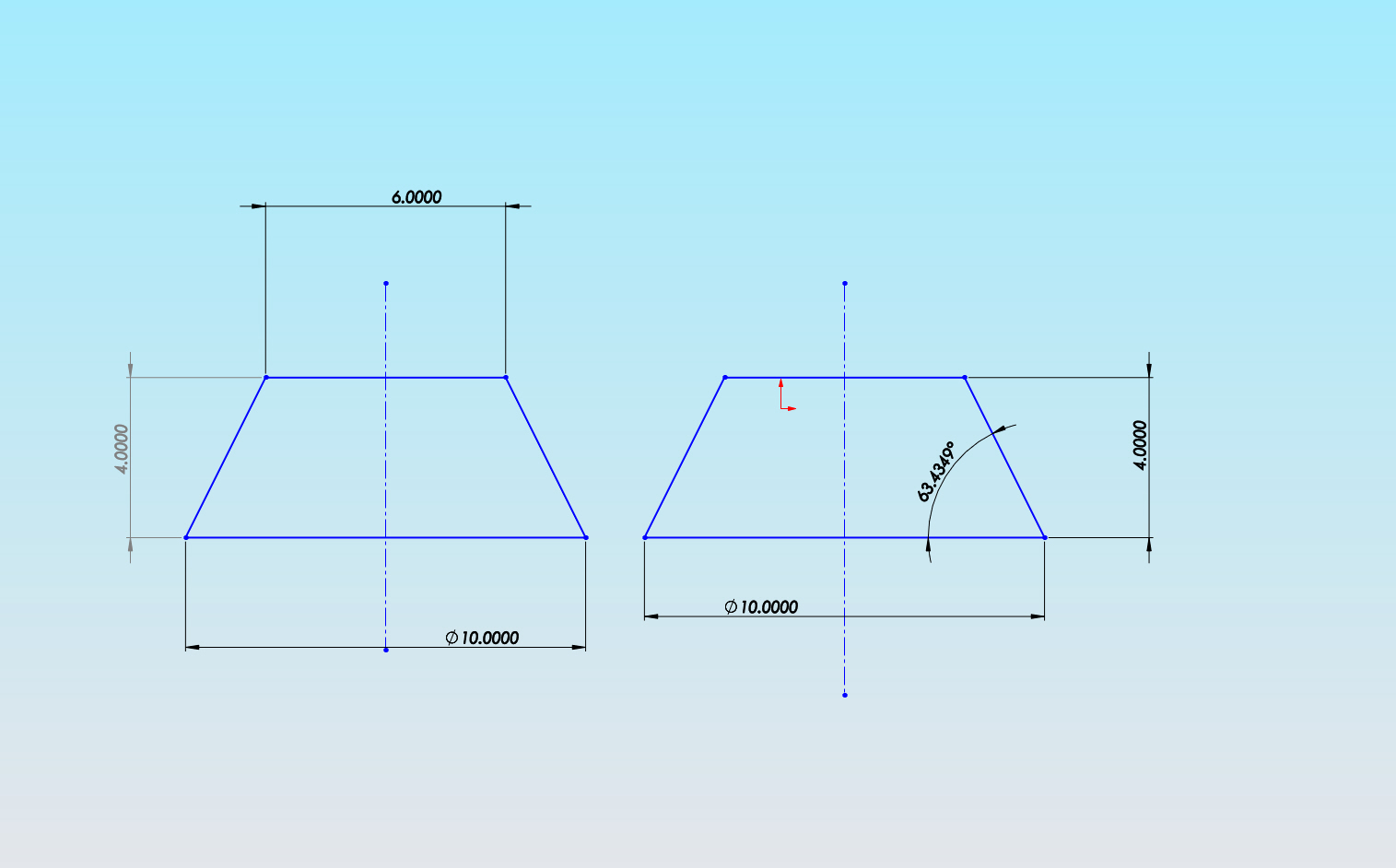



Solidworksで円錐台や円錐の作り方は




中学2年生です Clear
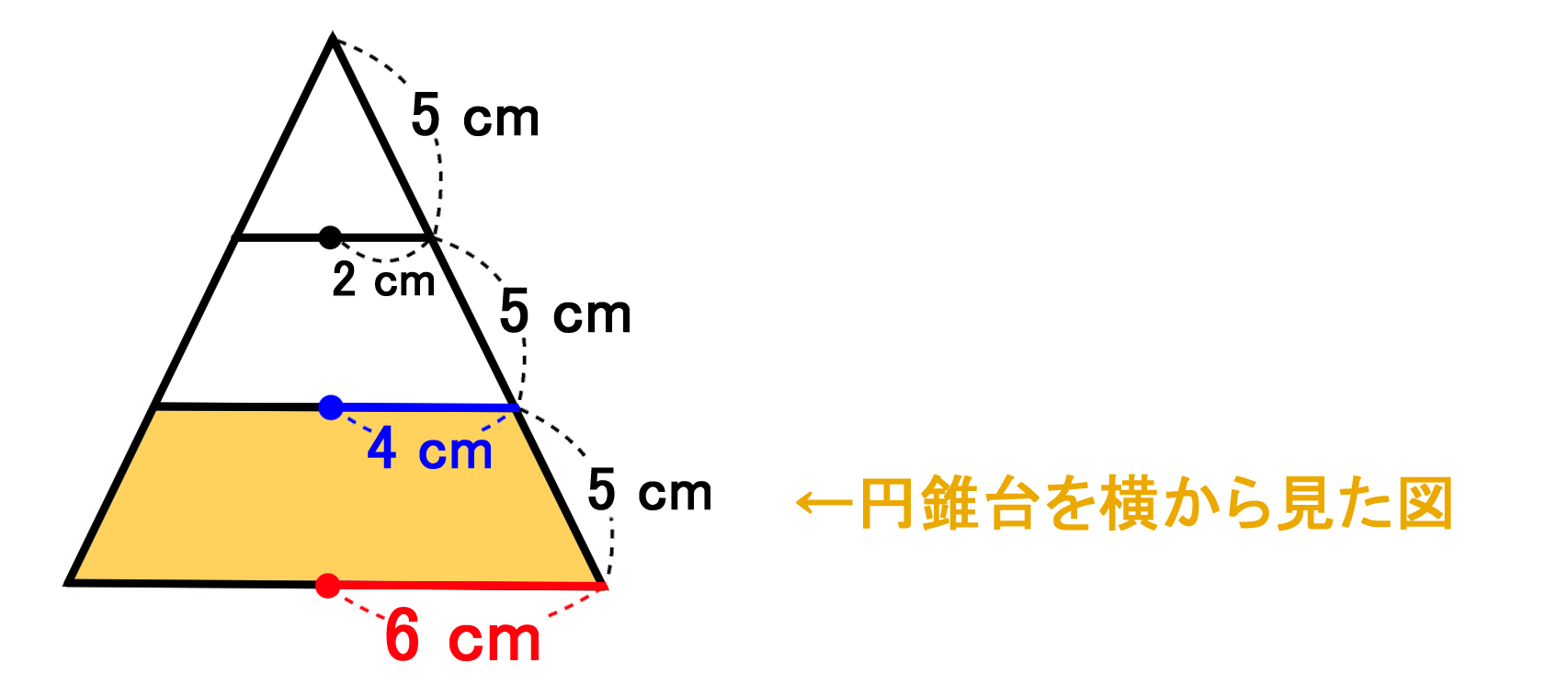



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




高校数学 直線の回転体の体積 回転一様双曲面 受験の月



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




Lr2jcikys9oefm



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




体積 の 求め 方 体積の公式は 1分でわかる求め方と覚え方 一覧 三角柱 円柱 三角錐の体積




体積比 回転体 Youtube




斜軸回転体の体積 応用編 傘型積分 おいしい数学




高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月



立派な 台形 体積 求め 方



Images Of 円錐台 Japaneseclass Jp




円錐 の 側 面積 の 求め 方 円すいの展開図 側面積の求め方 公式を使って15秒で解こう




円柱 体積 公式



Hd限定円錐 体積 の 求め 方 ページを着色するだけ




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ



立体図形 デジタル教科書 電子教科書
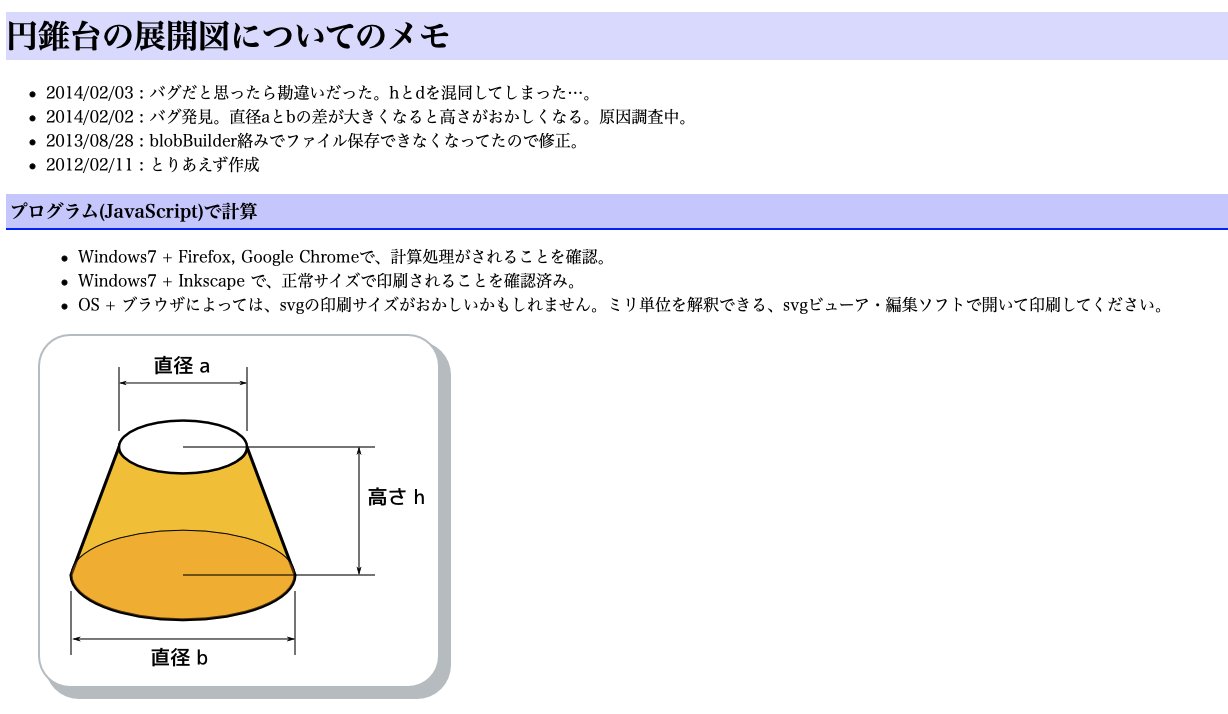



展開図 円錐台




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




円錐台 Wikipedia




17 号 フレキシブル基板及びそれを用いてなる円錐台形状の回路基板 Astamuse




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




05 号 ガラス体の延伸方法及び装置 Astamuse



円錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典
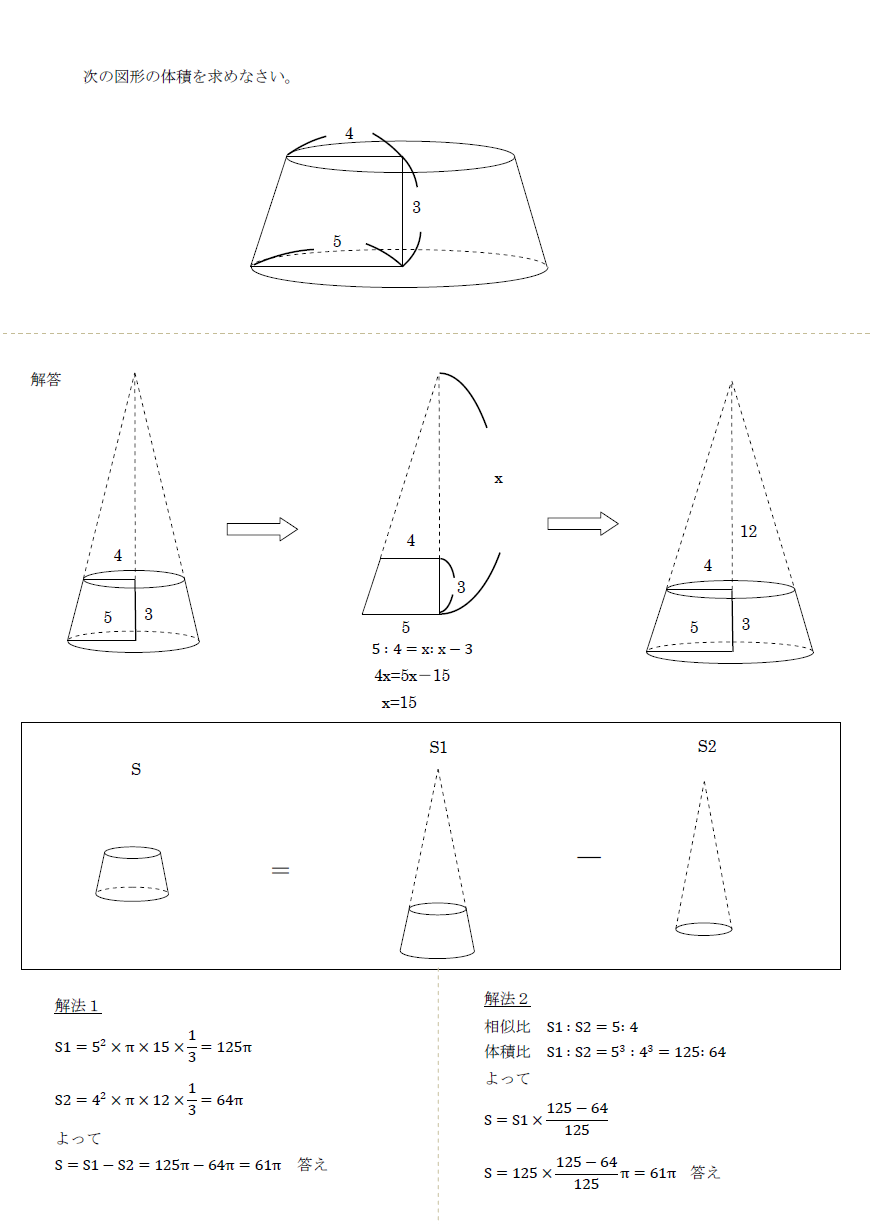



空間図形の体積 円錐台 の解法 中学 受験 定期試験 数学解き方集 裏技 解法



下の図のような立体を展開図にできますか 普通の円錐台の展開図は計算して作れ Yahoo 知恵袋
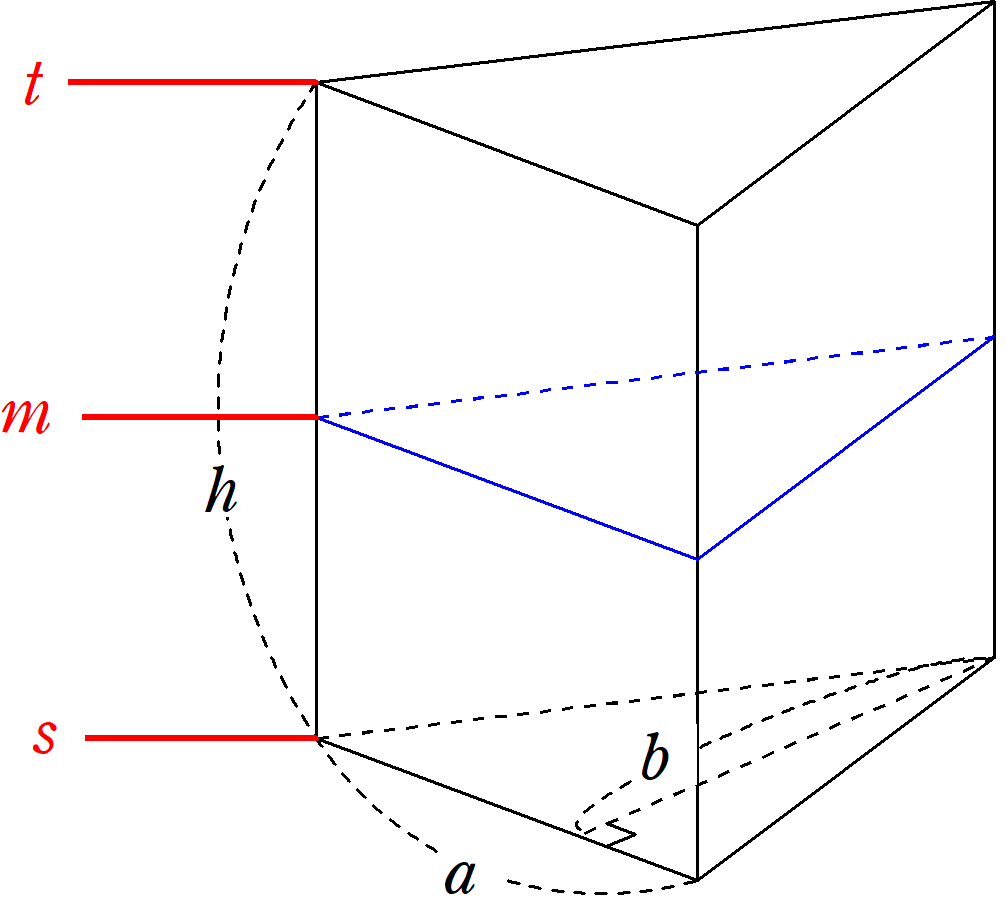



シンプソンの公式 応用編 Fukusukeの数学めも




毎日eトレ 762 円錐の体積を求める問題を解いているところです
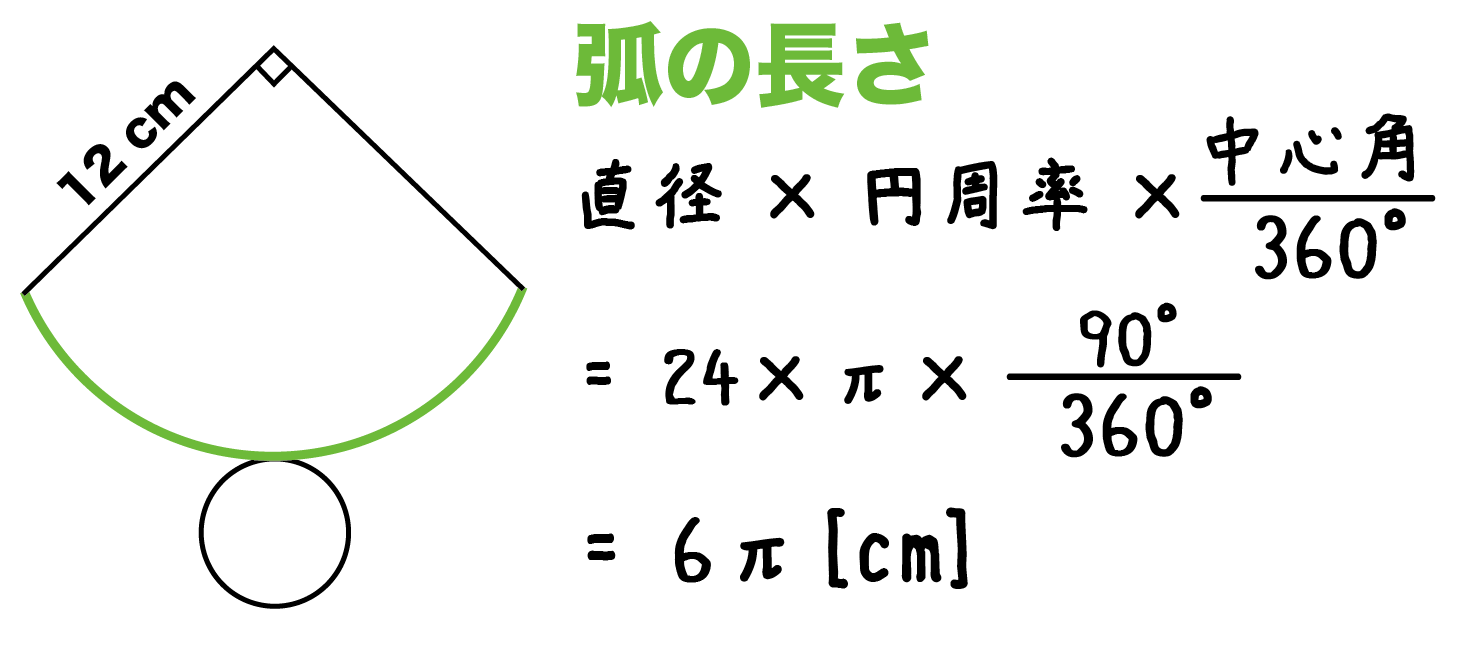



中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
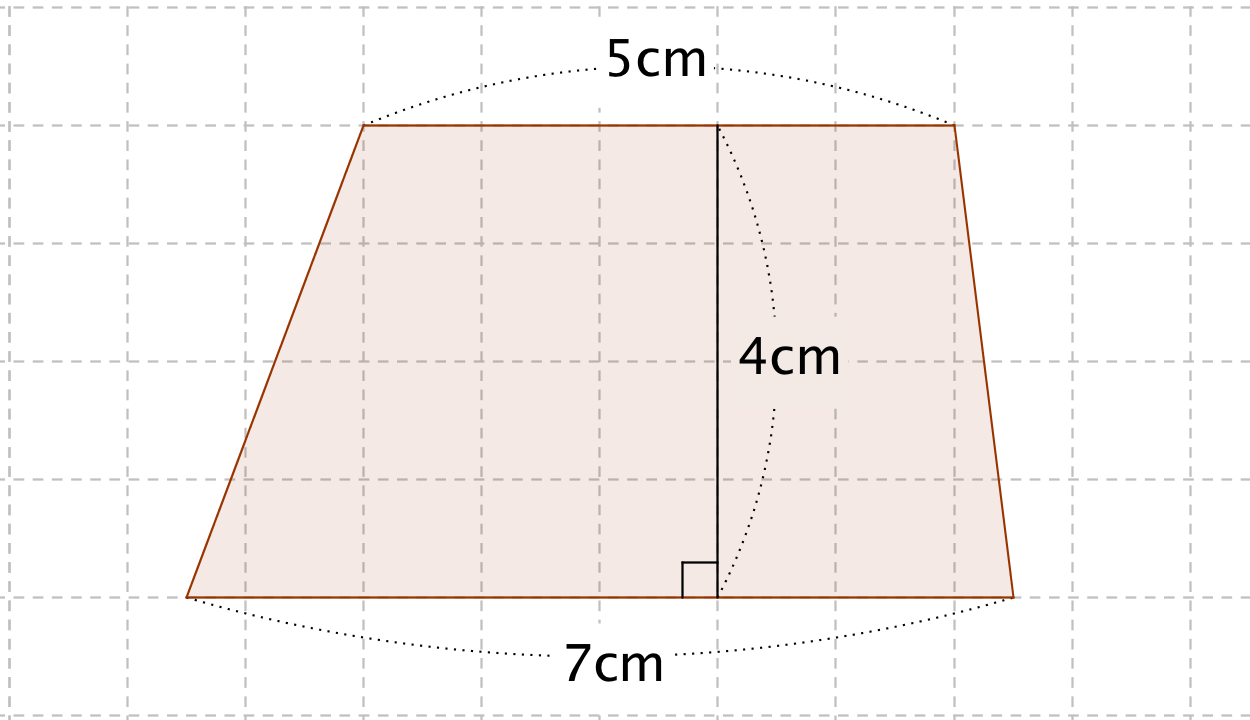



台形 体積 求め 方 円錐台の体積と表面積を計算する公式と証明




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



多角形の面積 重心 図心 断面n次モーメントの公式と 向き 頂点列の回転方向 の判別方法
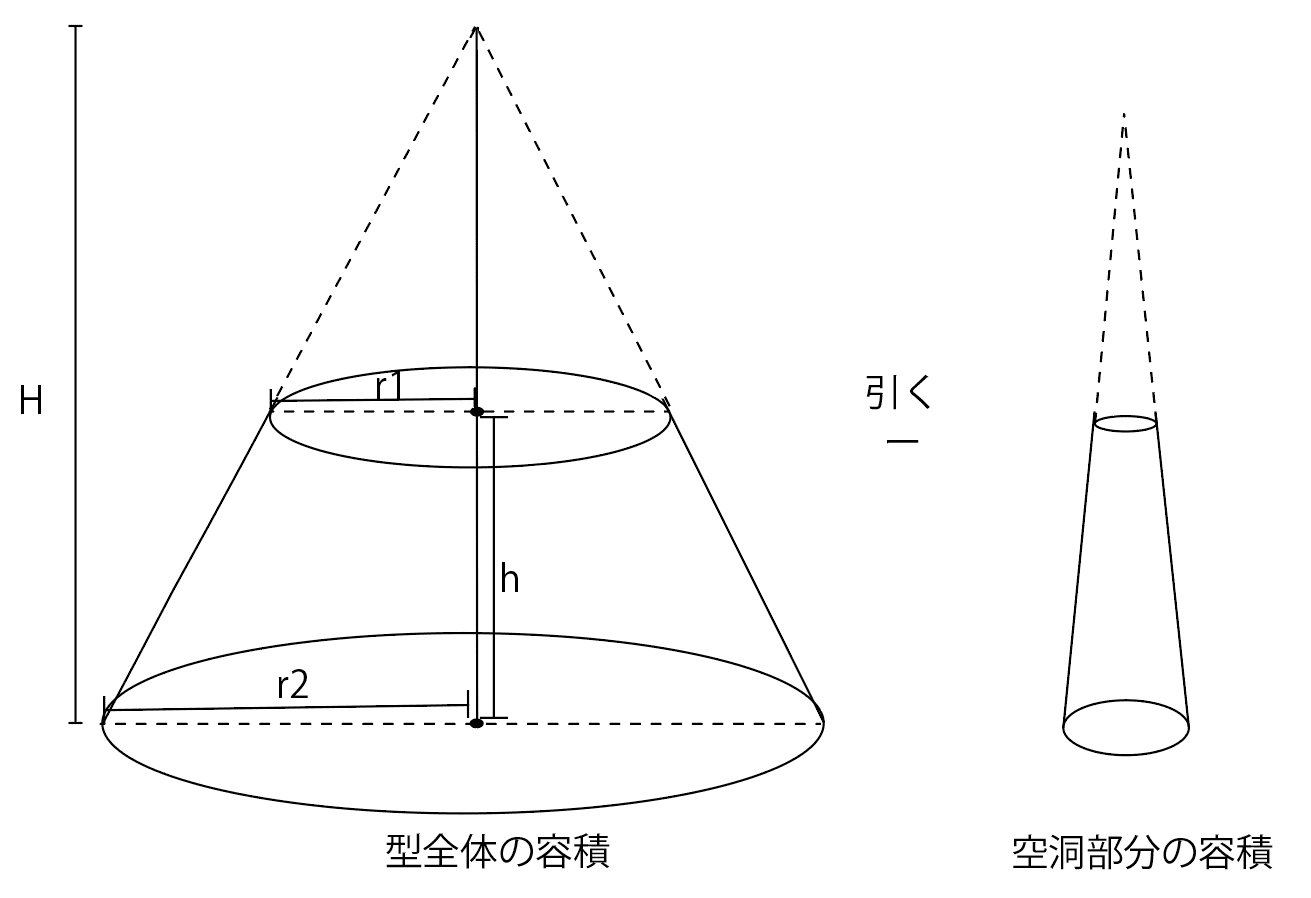



レシピと型のサイズが違う 型に必要な適性生地量は型比容積で計算しよう パン職人の朝は早い




図形計算機 Ease Labs




Images Of 円錐台 Japaneseclass Jp




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ
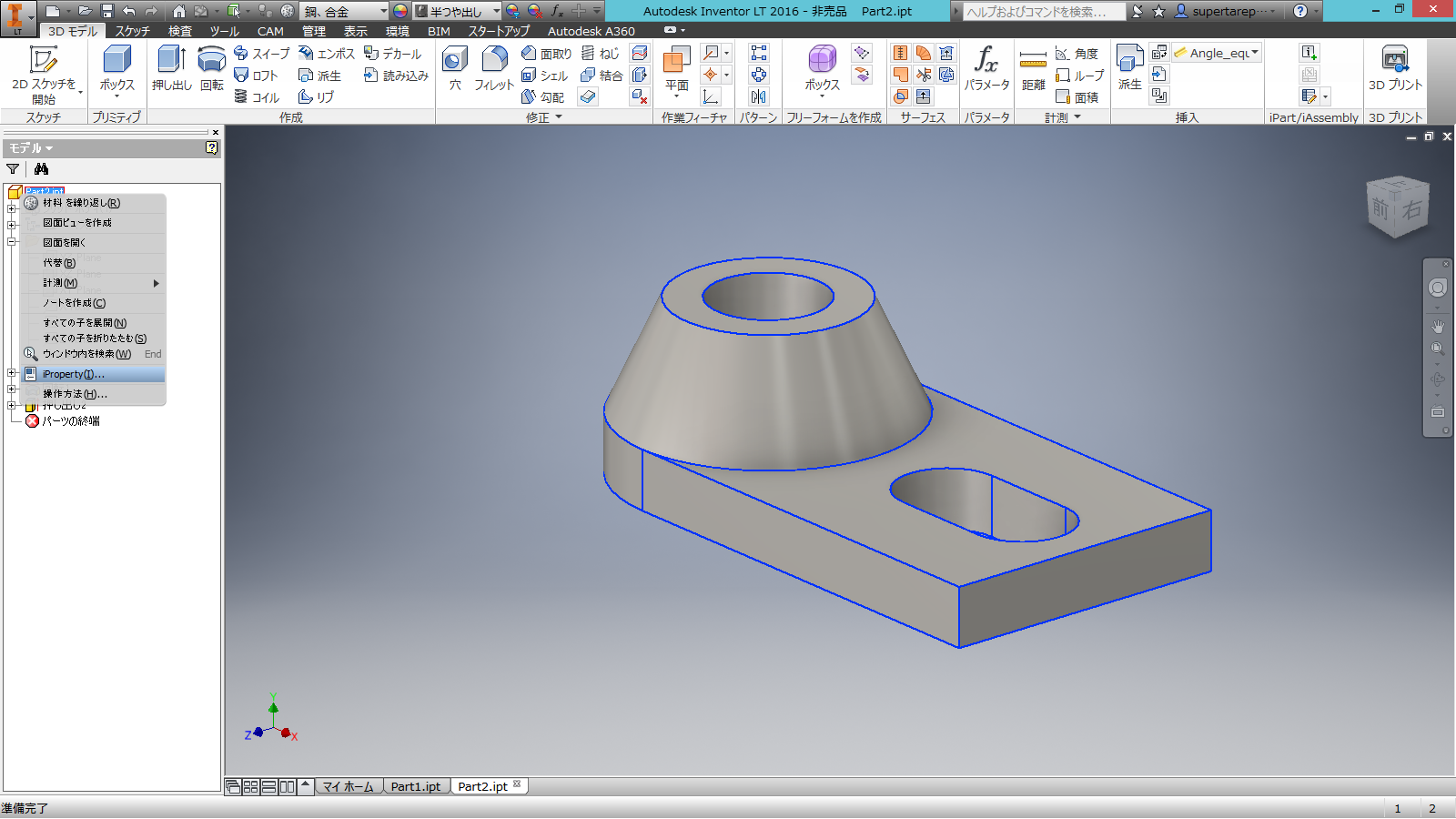



Autodesk Autocad Inventor Ltを触ってみよう 第3回 Born Digital Web Magazine




円錐 体積 の 求め 方 三平方の定理 円錐の高さが 体積を求める問題を解説


